Panel Fixed Effects for Causal Inference#

Panel data tracks the same units (workers, firms, countries) over multiple time periods. Fixed effects exploits this structure to control for unobserved confounders - either unit-specific characteristics, common time shocks, or both.

This notebook covers: when fixed effects identifies causal effects, how to implement it in CausalPy, and when it fails.

For a deeper treatment of panel data methods and causal inference, see Cunningham [2021] (Chapter 8), Huntington-Klein [2021], and Wooldridge [2010].

import warnings

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.linear_model import LinearRegression

import causalpy as cp

warnings.filterwarnings("ignore")

%config InlineBackend.figure_format = 'retina'
plt.style.use("default")

%load_ext autoreload
%autoreload 2

# Sampling settings for Bayesian models
sample_kwargs = {
    "draws": 2000,
    "tune": 1000,
    "chains": 4,
    "target_accept": 0.95,
    "random_seed": 42,
}

The Confounding Problem#

The standard panel data model is:

\[y_{it} = \beta D_{it} + u_i + \gamma_t + \epsilon_{it}\]

where \(D_{it}\) is treatment and \(\epsilon_{it}\) is idiosyncratic error. The terms \(u_i\) and \(\gamma_t\) are nuisance parameters we must account for to get an unbiased estimate of the causal effect \(\beta\):

\(u_i\) captures everything about unit \(i\) that is constant over time but affects the outcome (e.g., a worker’s innate ability, a firm’s culture). There is one \(u_i\) parameter per unit.
\(\gamma_t\) captures shocks at time \(t\) that affect all units equally (e.g., a recession, a policy change). There is one \(\gamma_t\) parameter per time period.

These become confounders if they also influence treatment assignment:

Confounder	What it is	Example	Solution
\(u_i\) (unit effect)	Time-invariant unit characteristics	Worker ability, firm culture	Unit FE
\(\gamma_t\) (time effect)	Common shocks affecting all units	Recessions, policy changes	Time FE

Without accounting for these, any correlation between \(D_{it}\) and \(u_i\) or \(\gamma_t\) biases our estimate. The DAG below illustrates both confounding paths:

../_images/76030549f0e4637d54e45327de652afe9b195f2382887775f8cac360bee79cff.svg

In summary, estimating the causal effect of treatment on the outcome risks bias from time-invariant unit effects, common temporal shocks, or both [Imai and Kim, 2019]. These confounders create backdoor paths. Normally we would close backdoor paths by conditioning, but we can’t do that directly here because they are unobserved. However, because these confounders have a specific structure (constant within units or across units), adding fixed effects can effectively close these backdoor paths.

The Fixed Effects Toolbox#

Fixed effects controls for confounders by comparing units to themselves (unit FE) or comparing across units within the same time period (time FE). The demeaned (de-meaned) transformation subtracts group means: \(\tilde{y}_{it} = y_{it} - \bar{y}_i\) absorbs \(u_i\) since \(u_i - \bar{u}_i = 0\).

FE Type	Controls for
Unit FE	\(u_i\) - time-invariant unit characteristics
Time FE	\(\gamma_t\) - common shocks affecting all units
Two-way FE	Both \(u_i\) and \(\gamma_t\)

Key assumptions for fixed effects to identify causal effects [Imai and Kim, 2019]:

Strict exogeneity: No feedback from past outcomes to current treatment
No time-varying confounders: Only time-invariant confounders exist (the key limitation!)
Treatment varies within units: Need some units to change treatment status over time
Parallel trends (for two-way FE): Connects to difference-in-differences assumptions

Example 1: One-Way Fixed Effects (Unit Only)#

This example demonstrates one-way unit fixed effects - we control for time-invariant unit characteristics but NOT for common time trends.

When is this appropriate?

Time trends are not a major concern (no common shocks affecting all units)
Or time effects are captured by covariates in the model
You want to preserve cross-sectional variation that time FE would remove

Let’s simulate panel data where we know the true treatment effect. This example is designed to satisfy all the identifying assumptions:

✅ Time-invariant confounders only (unit effects)
✅ No feedback from outcomes to treatment
✅ No time-varying confounders
✅ Treatment varies within units over time

Causal Question: What is the effect of treatment on the outcome, controlling for unobserved unit-level heterogeneity?

# Set up random number generator
rng = np.random.default_rng(42)

# Panel dimensions
n_units = 20
n_periods = 15
treatment_time = 10

# True parameters
TRUE_TREATMENT_EFFECT = 3.0
TRUE_X_COEF = 0.5

# Generate panel data
data = []
for i in range(n_units):
    unit_effect = rng.normal(scale=2.0)

    for t in range(n_periods):
        x1 = rng.normal()
        # First half of units get treated after treatment_time; second half are controls
        treatment = 1 if (t >= treatment_time and i < n_units // 2) else 0

        y = (
            unit_effect
            + TRUE_TREATMENT_EFFECT * treatment
            + TRUE_X_COEF * x1
            + rng.normal(scale=0.5)
        )

        data.append(
            {
                "unit": f"unit_{i}",
                "time": t,
                "treatment": treatment,
                "x1": x1,
                "y": y,
            }
        )

df_sim = pd.DataFrame(data)
print(f"Panel: {n_units} units, {n_periods} periods")
print(f"True treatment effect: {TRUE_TREATMENT_EFFECT}")
df_sim.head()

Panel: 20 units, 15 periods
True treatment effect: 3.0

	unit	time	x1	y
0	unit_0	0	-1.039984	0.464668
1	unit_0	1	0.940565	0.104199
2	unit_0	2	-1.302180	0.022265
3	unit_0	3	-0.316243	0.442912
4	unit_0	4	-0.853044	0.622611

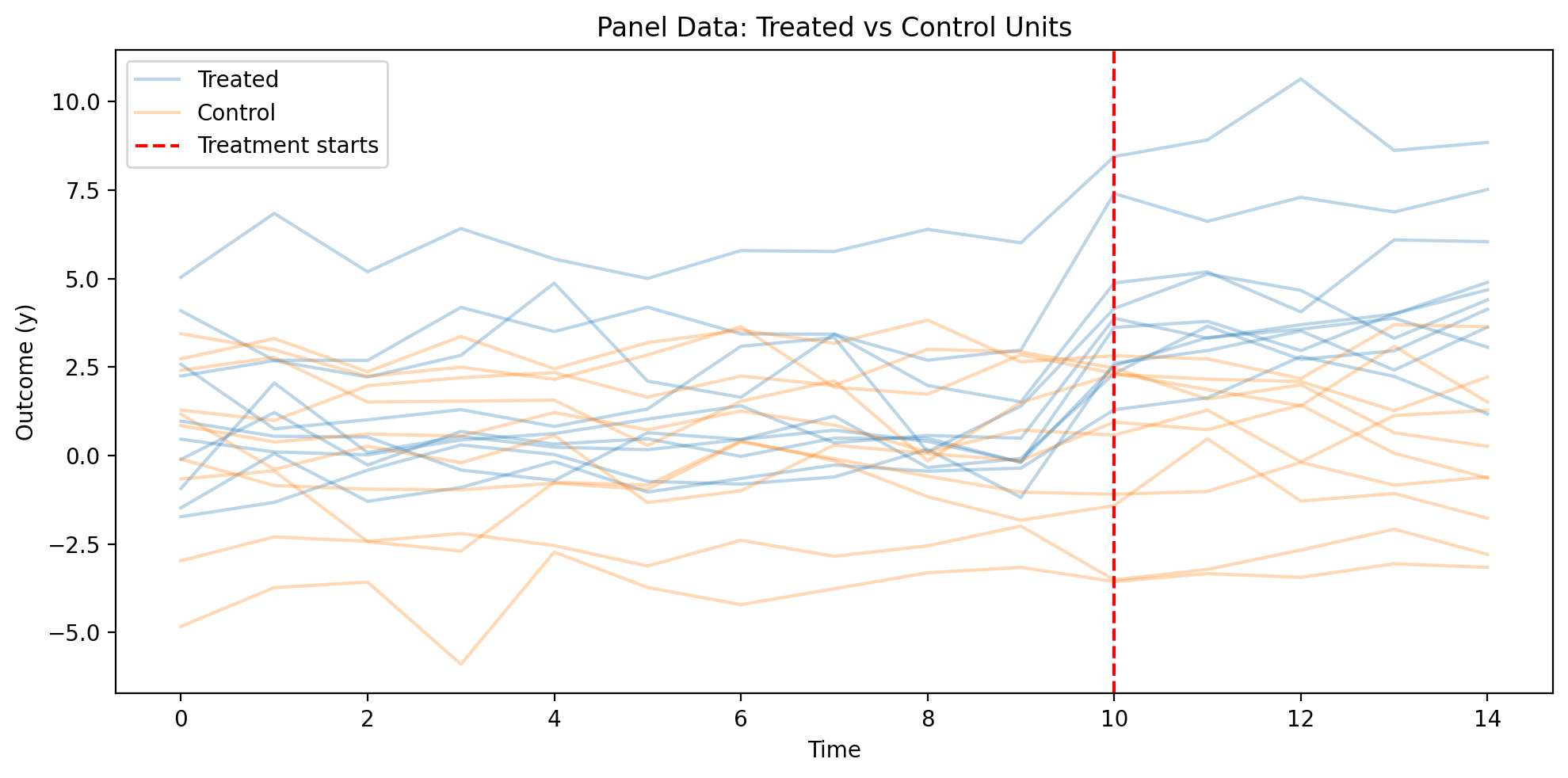
../_images/2a1d2ae2a13e6625adbf8f7a52b49ed04162645677440d77b37ae19c568f911d.png

Naive OLS (Biased)#

First, let’s see what happens if we ignore the unit fixed effects:

# Naive OLS without fixed effects
X_naive = df_sim[["treatment", "x1"]].values
y_naive = df_sim["y"].values

naive_model = LinearRegression().fit(X_naive, y_naive)
print("Naive OLS (NO fixed effects):")
print(f"  Treatment effect: {naive_model.coef_[0]:.3f} (True: {TRUE_TREATMENT_EFFECT})")
print(f"  Bias: {naive_model.coef_[0] - TRUE_TREATMENT_EFFECT:.3f}")

Naive OLS (NO fixed effects):
  Treatment effect: 3.796 (True: 3.0)
  Bias: 0.796

Fixed Effects with Dummies#

# One-way unit FE with dummy variables (Bayesian)
# Note: time_fe_variable is not set, so we only control for unit effects
result_dummies = cp.PanelRegression(
    data=df_sim,
    formula="y ~ C(unit) + treatment + x1",  # No C(time) - unit FE only
    unit_fe_variable="unit",
    fe_method="dummies",
    model=cp.pymc_models.LinearRegression(sample_kwargs=sample_kwargs),
)

result_dummies.summary()

Panel Regression
============================================================
Units: 20 (unit)
FE method: dummies
Observations: 300
============================================================

Note: 19 fixed effect coefficients not shown (use print_coefficients() to see all)

Model Coefficients:
Model coefficients:
    Intercept    0.75, 94% HDI [0.49, 1]
    treatment    3.1, 94% HDI [2.9, 3.3]
    x1           0.5, 94% HDI [0.44, 0.56]
    y_hat_sigma  0.51, 94% HDI [0.47, 0.56]

The treatment effect estimate (treatment 3.1, 94% HDI [2.9, 3.3]) closely recovers the true value of 3.0, and the 94% HDI contains the true parameter. This demonstrates that one-way unit fixed effects successfully removes the bias from time-invariant unit confounders \(u_i\).

Fixed Effects with Demeaned Transformation#

The demeaned transformation gives identical results:

# One-way unit FE with demeaned transformation (Bayesian)
# Note: time_fe_variable is not set, so we only control for unit effects
result_demeaned = cp.PanelRegression(
    data=df_sim,
    formula="y ~ treatment + x1",  # No C(unit) needed with demeaned transformation!
    unit_fe_variable="unit",
    # time_fe_variable not set = one-way unit FE
    fe_method="demeaned",
    model=cp.pymc_models.LinearRegression(sample_kwargs=sample_kwargs),
)

result_demeaned.summary()

Panel Regression
============================================================
Units: 20 (unit)
FE method: demeaned
Observations: 300
============================================================

Model Coefficients:
Model coefficients:
    Intercept    1.1e-05, 94% HDI [-0.054, 0.053]
    treatment    3.1, 94% HDI [3, 3.3]
    x1           0.5, 94% HDI [0.44, 0.56]
    y_hat_sigma  0.5, 94% HDI [0.46, 0.54]

Interpreting the Results#

The treatment coefficient of approximately 3.1 (true value: 3.0) represents the within-unit causal effect of treatment on the outcome.

What this means: For the same unit, receiving treatment increases the outcome by about 3 units on average, after controlling for all time-invariant unit characteristics.

Key insight: This estimate comes from comparing each unit to itself at different time points - not from comparing treated units to control units. This is why fixed effects can control for unobserved unit-level confounders.

The Bayesian credible interval provides uncertainty quantification: we’re 94% confident the true effect lies within this range.

Comparing One-Way vs Two-Way Fixed Effects#

Recall that our simulated data includes unit-specific confounders (\(u_i\)) but no common time shocks (\(\gamma_t\)) that affect all units equally. What happens if we add time fixed effects anyway? Let’s compare:

One-way (unit only): What we just estimated above
Two-way (unit + time): Adding time fixed effects

Since there are no time shocks in this data, we expect both estimates to be similar. This illustrates that adding unnecessary fixed effects doesn’t bias estimates—but it does consume degrees of freedom.

# Two-way FE: Add time fixed effects to the same data
result_twoway = cp.PanelRegression(
    data=df_sim,
    formula="y ~ treatment + x1",  # Demeaned transformation handles both unit and time
    unit_fe_variable="unit",
    time_fe_variable="time",  # <-- This adds time FE!
    fe_method="demeaned",
    model=cp.pymc_models.LinearRegression(sample_kwargs=sample_kwargs),
)

# Compare the treatment effect estimates
print("=" * 60)
print("COMPARISON: One-Way vs Two-Way Fixed Effects")
print("=" * 60)
print(f"\nTrue treatment effect: 3.0")
print(f"\nOne-way (unit FE only):")
print(
    f"  Treatment coefficient: {result_demeaned.model.idata.posterior['beta'].sel(coeffs='treatment').mean().values:.3f}"
)
print(f"\nTwo-way (unit + time FE):")
print(
    f"  Treatment coefficient: {result_twoway.model.idata.posterior['beta'].sel(coeffs='treatment').mean().values:.3f}"
)
print("\nIn this case, both estimates are similar because the simulated data")
print("doesn't have strong common time trends that confound treatment.")

============================================================
COMPARISON: One-Way vs Two-Way Fixed Effects
============================================================

True treatment effect: 3.0

One-way (unit FE only):
  Treatment coefficient: 3.120

Two-way (unit + time FE):
  Treatment coefficient: 3.071

In this case, both estimates are similar because the simulated data
doesn't have strong common time trends that confound treatment.

Tip

When does the choice matter?

The estimates from one-way and two-way FE will differ when:

There are common time shocks (e.g., a recession affecting all units) that correlate with treatment
Treatment rollout is correlated with time trends (e.g., early adopters vs late adopters)

If neither condition applies, one-way unit FE is often sufficient and more parsimonious.

Example 2: When Fixed Effects Fails#

The simulation above worked because our data satisfied all the identifying assumptions. But what happens when those assumptions are violated? We continue with one-way unit fixed effects to isolate the problem.

Here we add a time-varying confounder—an economic shock that varies by unit and time—that affects both treatment and outcome. Workers are more likely to seek training during good economic times, and the shock also directly affects productivity. Unit fixed effects cannot remove this confounder because it changes over time, and time fixed effects cannot remove it either because it varies across units. No combination of fixed effects can eliminate confounders that vary in both dimensions.

# Simulate data with a TIME-VARYING confounder
rng = np.random.default_rng(42)

n_units = 20
n_periods = 15
TRUE_TREATMENT_EFFECT = 3.0  # Same as before

data_violation = []
for i in range(n_units):
    unit_effect = rng.normal(scale=2.0)  # Time-invariant (FE handles this)

    for t in range(n_periods):
        # TIME-VARYING confounder: an economic shock that varies by unit AND time
        economic_shock = rng.normal(scale=1.5)

        # Treatment is AFFECTED by the economic shock (more likely to train during good times)
        treatment_propensity = 0.3 + 0.3 * (economic_shock > 0)
        treatment = 1 if (rng.random() < treatment_propensity and t >= 5) else 0

        # Outcome is affected by treatment AND the economic shock
        y = (
            unit_effect
            + TRUE_TREATMENT_EFFECT * treatment
            + 2.0 * economic_shock  # Direct effect of confounder on outcome
            + rng.normal(scale=0.5)
        )

        data_violation.append(
            {"unit": f"unit_{i}", "time": t, "treatment": treatment, "y": y}
        )

df_violation = pd.DataFrame(data_violation)

# Apply fixed effects
result_violation = cp.PanelRegression(
    data=df_violation,
    formula="y ~ treatment",
    unit_fe_variable="unit",
    fe_method="demeaned",
    model=LinearRegression(),
)

============================================================
FIXED EFFECTS WITH TIME-VARYING CONFOUNDER
============================================================
True treatment effect:      3.00
FE estimate:                3.93
Bias:                       0.93

⚠️  The estimate is BIASED because the economic shock
   affects both treatment and outcome, and FE cannot remove it!
============================================================

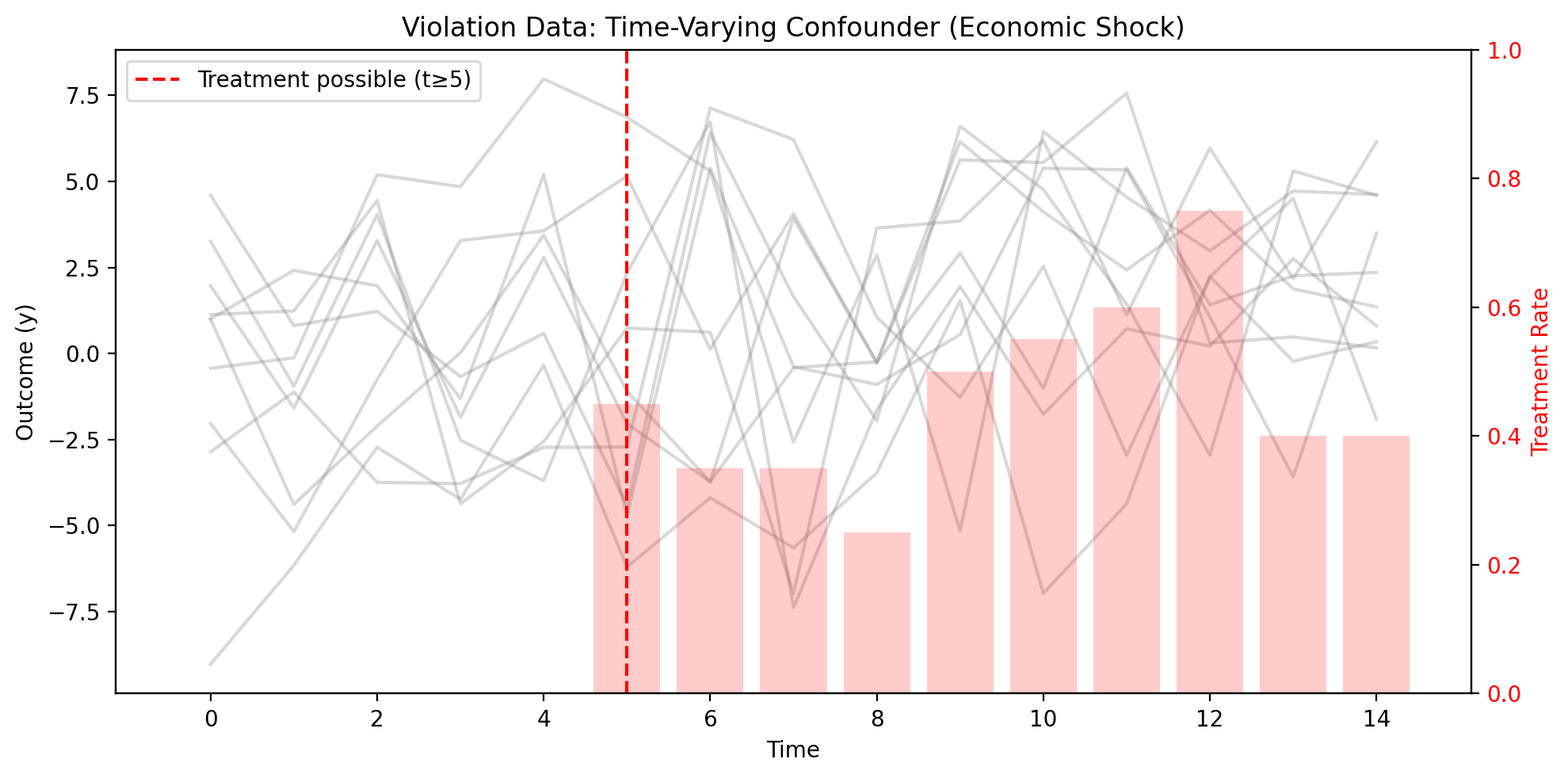
../_images/f1147d4eb82fc56f7c811e563462b1f8bf8e84e7261c7b5209a42c81a0826079.png

The plot shows individual unit trajectories (gray lines) with the treatment rate at each time period (red bars). Notice how treatment probability increases over time—but this isn’t random. Units experiencing positive economic shocks are both more likely to be treated and have higher outcomes, creating confounding that fixed effects cannot remove.

This example demonstrates a critical limitation: fixed effects only removes time-invariant confounders. In DAG terms, adding a time-varying confounder \(v_{it}\) creates an open backdoor path that fixed effects cannot close:

../_images/bdbdef7e1dac2ee7c5b6d131aaf36781d573d00c5c5553b1b43e75dbcf61e7d1.svg

Fixed effects eliminates the \(u_i\) backdoor path (gray, dashed) but not the \(v_{it}\) path (red). The estimate remains biased.

Important

Before using fixed effects, ask yourself: Are there any unobserved factors that change over time and affect both my treatment and outcome? If yes, fixed effects alone is insufficient.

Connection to Difference-in-Differences#

Two-way fixed effects (TWFE) - with both unit and time fixed effects - is closely related to difference-in-differences (DiD).

With a simple 2x2 design (2 groups, 2 periods, binary treatment), TWFE produces numerically identical estimates to the classic DiD estimator. The model:

\[Y_{it} = \alpha_i + \gamma_t + \beta \cdot D_{it} + \epsilon_{it}\]

where:

\(\alpha_i\) = unit fixed effects
\(\gamma_t\) = time fixed effects
\(D_{it}\) = treatment indicator

is a workhorse of applied causal inference. The coefficient \(\beta\) captures the treatment effect.

With more complex designs (staggered treatment adoption, heterogeneous effects), TWFE and simple DiD can diverge. Recent econometrics research [de Chaisemartin and D'Haultfœuille, 2020] has highlighted that TWFE can give misleading results when:

Treatment effects vary over time (dynamic effects)
Treatment rolls out at different times (staggered adoption)
Treatment effects differ across units (heterogeneity)

For these cases, consider using CausalPy’s DifferenceInDifferences class or newer estimators designed for staggered designs.

Example 3: Two-Way Fixed Effects (Unit + Time)#

Two-way fixed effects (TWFE) is the workhorse model in applied economics and the foundation of difference-in-differences analysis.

Causal Question: What is the effect of a state policy on outcomes, controlling for both state-specific factors and common time trends?

This example uses two-way fixed effects (state + year FE), which controls for:

Time-invariant state characteristics (state FE) — e.g., geography, political culture
Common shocks affecting all states in a given year (year FE) — e.g., national economic conditions

When to use two-way FE:

Treatment timing varies across units (staggered adoption)
Common time shocks could confound the treatment-outcome relationship
You’re doing a difference-in-differences style analysis

For small panels (e.g., 50 US states), we can use the dummy variable approach.

# Simulate state-level data
rng = np.random.default_rng(123)

n_states = 12
n_years = 10
policy_year = 5

state_data = []
for s in range(n_states):
    state_name = f"State_{chr(65 + s)}"
    state_baseline = rng.normal(loc=50, scale=5)

    for y in range(n_years):
        policy = 1 if (y >= policy_year and s < n_states // 2) else 0
        gdp_growth = rng.normal(scale=2)

        outcome = (
            state_baseline
            + 0.3 * y
            + 5.0 * policy
            + 0.5 * gdp_growth
            + rng.normal(scale=1.5)
        )

        state_data.append(
            {
                "state": state_name,
                "year": y,
                "policy": policy,
                "gdp_growth": gdp_growth,
                "outcome": outcome,
            }
        )

df_states = pd.DataFrame(state_data)
print(f"State panel: {n_states} states, {n_years} years")
df_states.head()

State panel: 12 states, 10 years

	state	year	gdp_growth	outcome
0	State_A	0	-0.735573	46.618494
1	State_A	1	0.387949	46.928714
2	State_A	2	1.154208	45.276802
3	State_A	3	1.083904	46.021452
4	State_A	4	-0.644778	46.077755

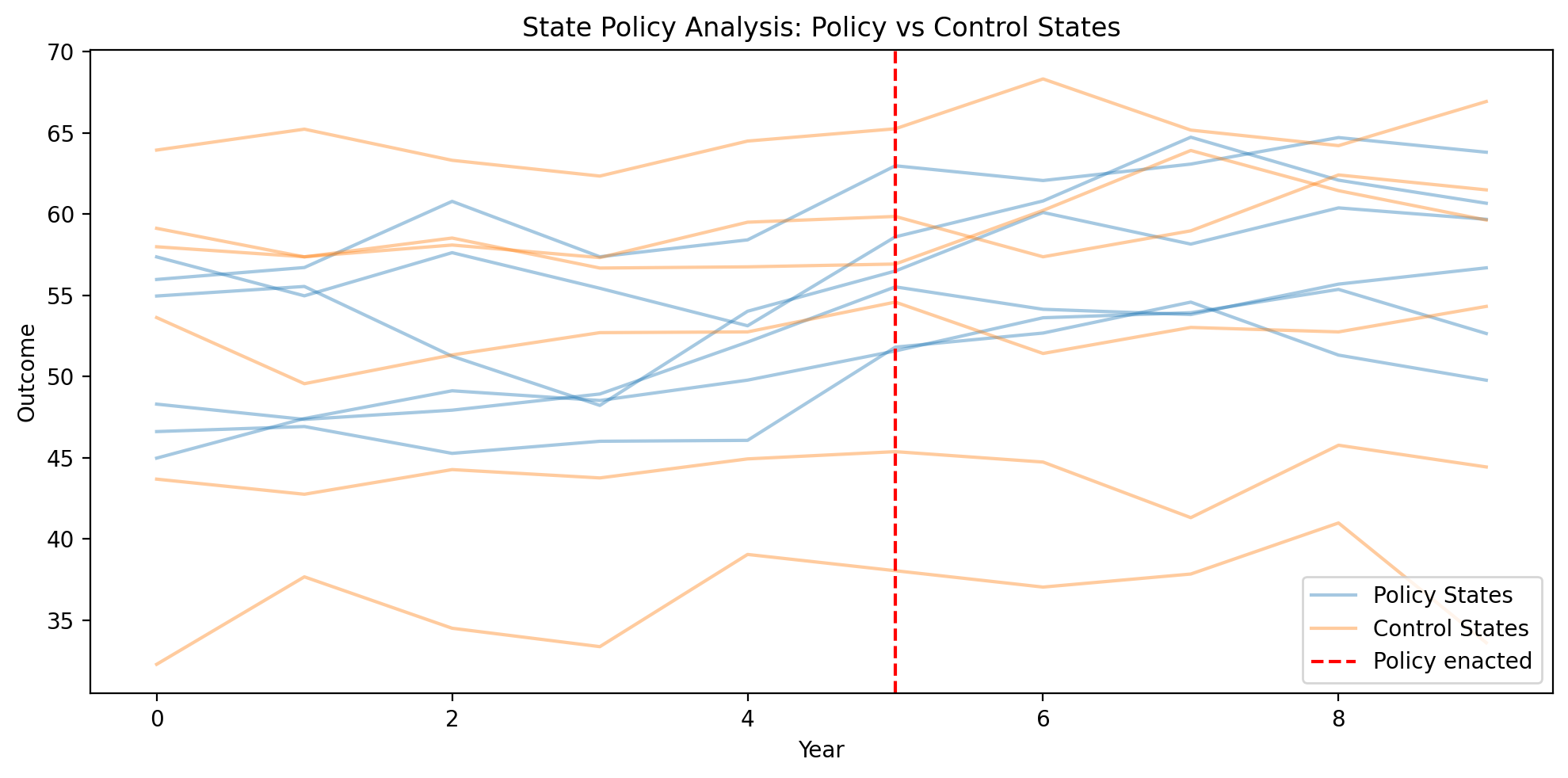
../_images/a64e6154bf5d81e9c6491c2a400dbc47a39bb3fbbca749a078997ff02e4a6948.png

# Fit panel regression with state and year FE (Bayesian)
result_states = cp.PanelRegression(
    data=df_states,
    formula="outcome ~ C(state) + C(year) + policy + gdp_growth",
    unit_fe_variable="state",
    time_fe_variable="year",
    fe_method="dummies",
    model=cp.pymc_models.LinearRegression(sample_kwargs=sample_kwargs),
)

result_states.summary()

Panel Regression
============================================================
Units: 12 (state)
Periods: 10 (year)
FE method: dummies
Observations: 120
============================================================

Note: 20 fixed effect coefficients not shown (use print_coefficients() to see all)

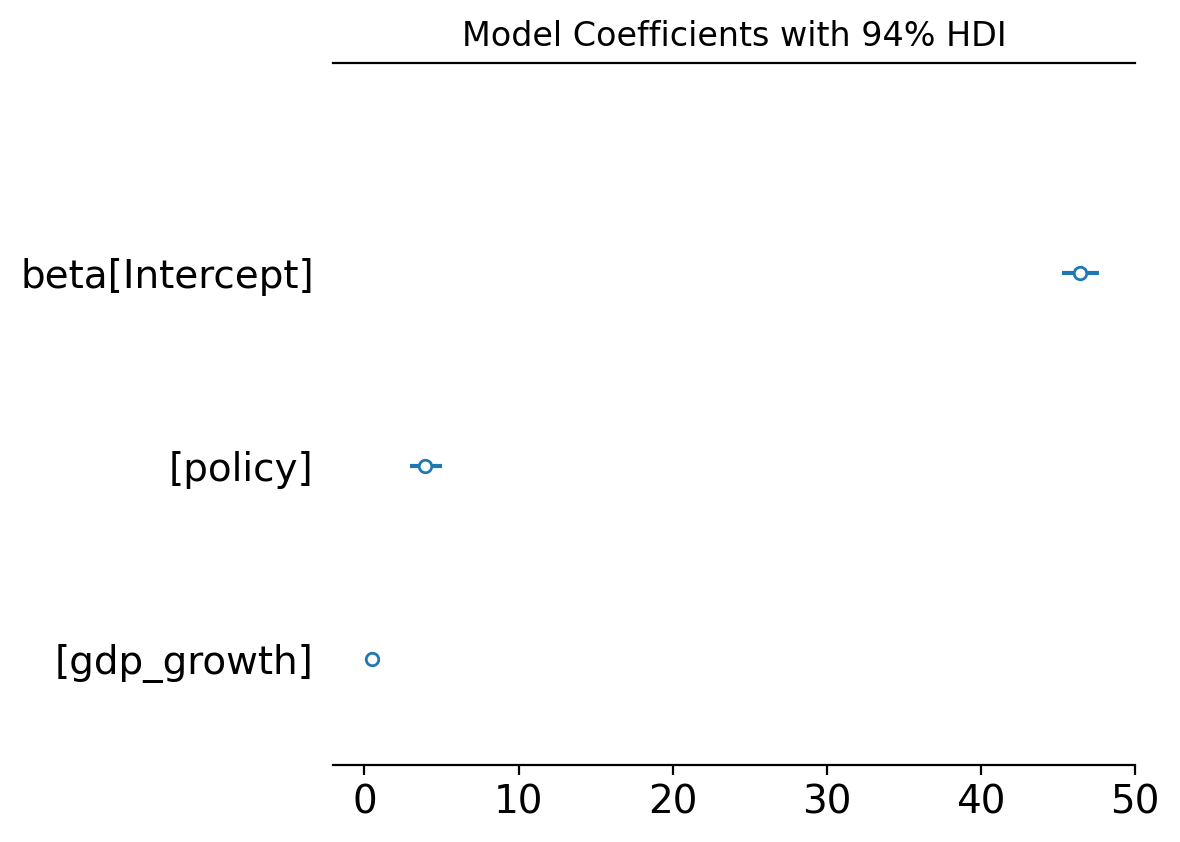
Model Coefficients:
Model coefficients:
    Intercept    46, 94% HDI [45, 48]
    policy       3.9, 94% HDI [2.9, 5]
    gdp_growth   0.48, 94% HDI [0.33, 0.63]
    y_hat_sigma  1.5, 94% HDI [1.3, 1.7]

# Coefficient plot
fig, ax = result_states.plot_coefficients()
plt.tight_layout()
plt.show()

../_images/646accf462f3676542812bf70ce0a0ef1e4c2e218fe576e05244dc41618f627f.png

# Distribution of state fixed effects
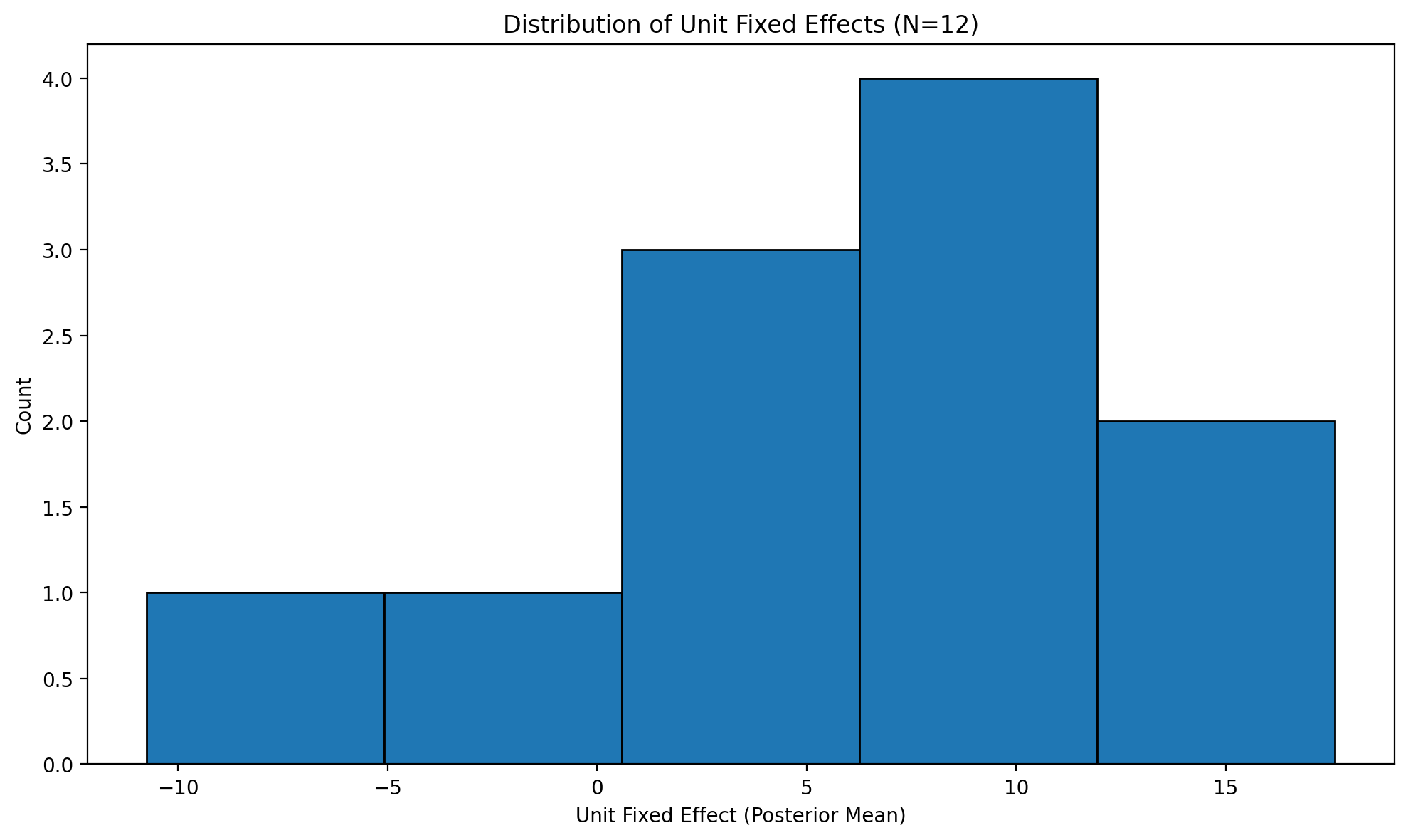
fig, ax = result_states.plot_unit_effects()
plt.tight_layout()
plt.show()

../_images/b7e8becbeecfefea330aa5d813c31b1c48e43eff91577c3902673c7cad8514e4.png

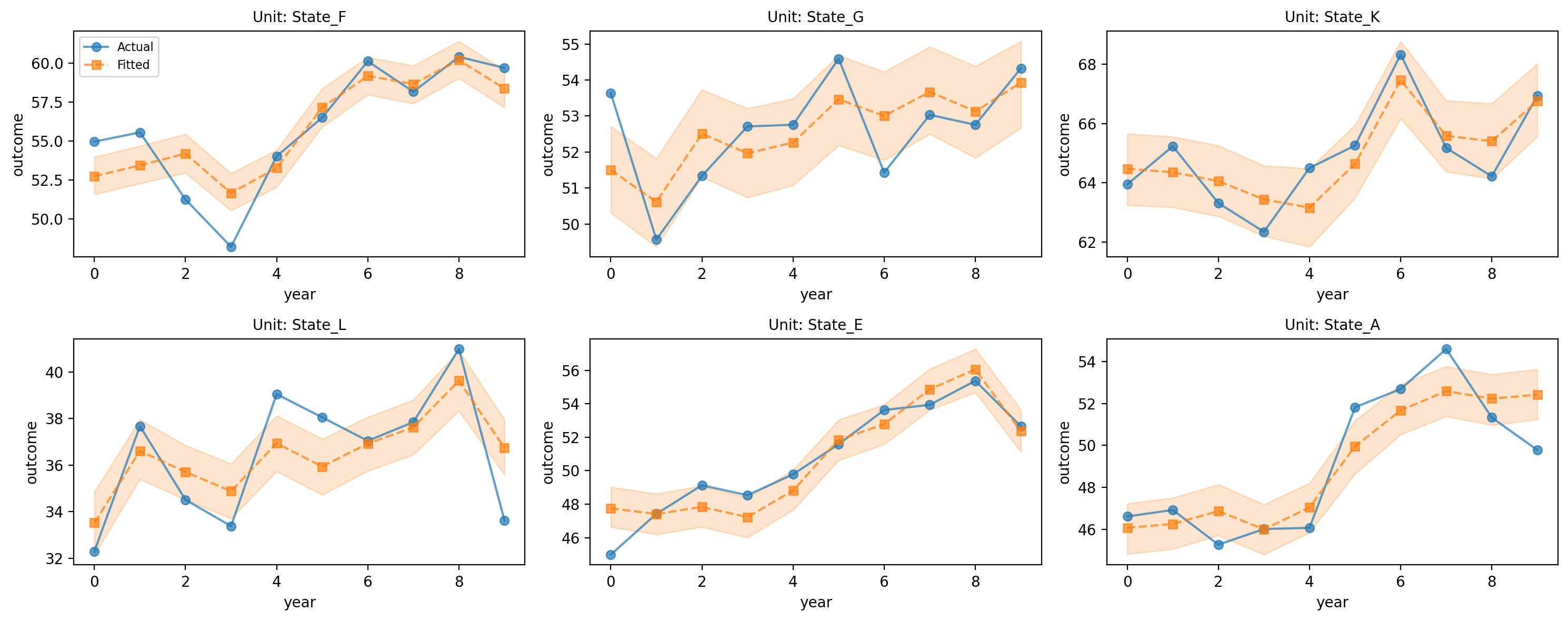
# State trajectories
fig, axes = result_states.plot_trajectories(n_sample=6)
plt.tight_layout()
plt.show()

../_images/c5a0ee3fb6a464c4dd0a69a1cbe0d0efe3548589aad182faedc751e2e7a11b51.png

Example 4: Two-Way FE with Large Panel (Demeaned Transformation)#

With 200 workers, including dummy variables for each would add 199 coefficients to our model—slow to estimate and cluttering output with nuisance parameters we don’t care about. The demeaned transformation solves this by subtracting group means before estimation, effectively sweeping out the fixed effects without explicitly estimating them.

Causal Question: What is the effect of job training on worker productivity?

This is our motivating example from the introduction! Workers who receive training may differ in unobserved ability - the classic selection problem.

Why two-way FE here?

Worker FE: Controls for innate ability (time-invariant)
Wave FE: Controls for economy-wide conditions affecting all workers

Assumptions we’re making:

Innate ability is time-invariant (plausible)
No time-varying confounders (e.g., no unobserved motivation shocks)
Training doesn’t respond to recent productivity changes

# Simulate worker panel
rng = np.random.default_rng(456)

n_workers = 200
n_waves = 8
training_wave = 4

worker_data = []
for w in range(n_workers):
    worker_id = f"worker_{w:04d}"
    ability = rng.normal(scale=3)

    for wave in range(n_waves):
        trained = 1 if (wave >= training_wave and w < n_workers * 0.4) else 0
        experience = wave * 0.5 + rng.normal(scale=0.2)

        productivity = (
            ability + 2.5 * trained + 0.3 * experience + rng.normal(scale=0.8)
        )

        worker_data.append(
            {
                "worker_id": worker_id,
                "wave": wave,
                "trained": trained,
                "experience": experience,
                "productivity": productivity,
            }
        )

df_workers = pd.DataFrame(worker_data)
print(f"Worker panel: {n_workers} workers, {n_waves} waves")
df_workers.head()

Worker panel: 200 workers, 8 waves

	worker_id	wave	trained	experience	productivity
0	worker_0000	0	0	-0.424790	3.872846
1	worker_0000	1	0	0.492939	0.753789
2	worker_0000	2	0	0.961987	2.445428
3	worker_0000	3	0	1.417059	2.879282
4	worker_0000	4	1	2.389001	6.709637

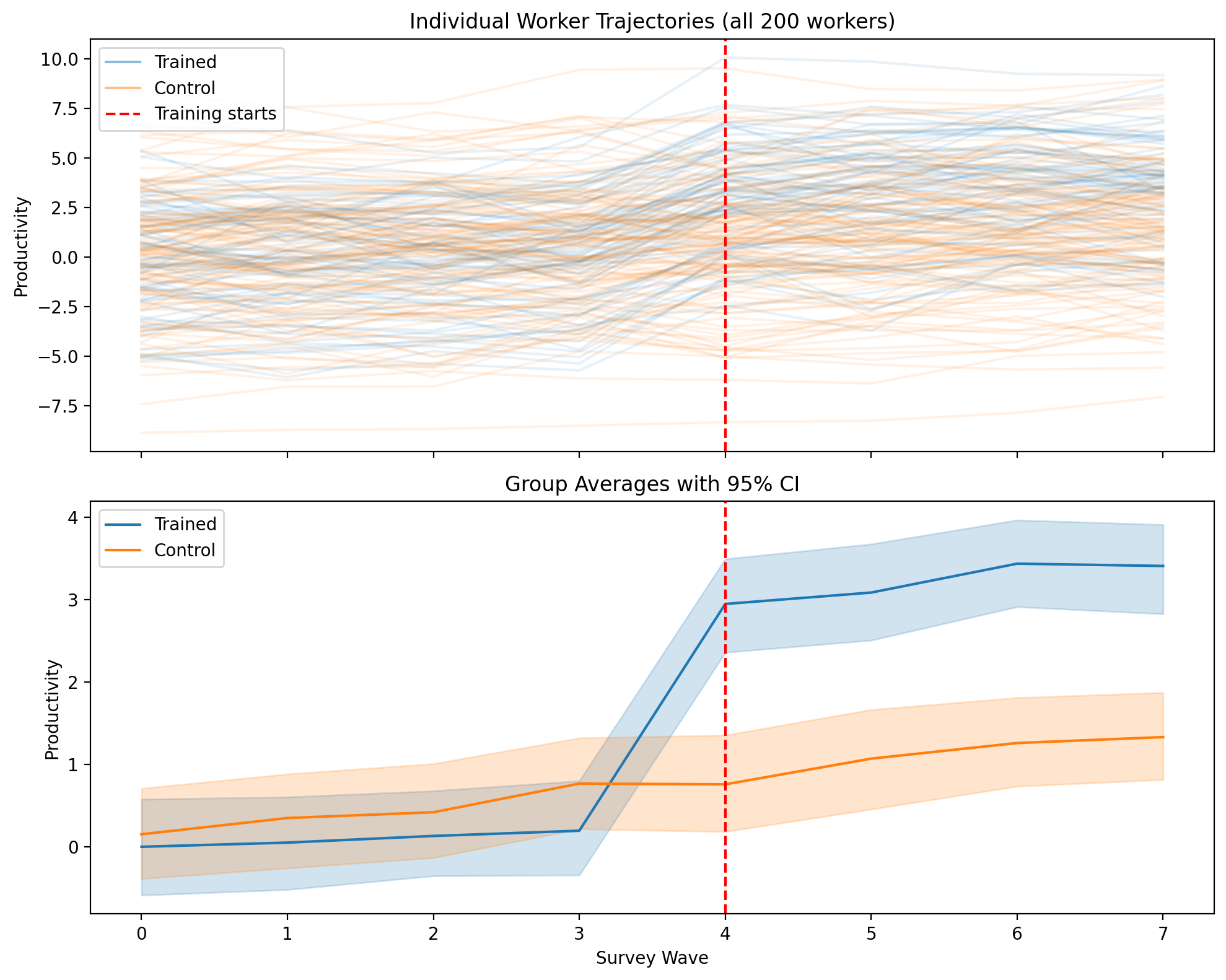
../_images/056531129edd6455ae0bc6bccb03aaee48e50262b6370f74a536dfae440fae06.png

# Two-way FE with demeaned transformation (Bayesian)
# Both worker_id and wave are used for fixed effects
result_workers = cp.PanelRegression(
    data=df_workers,
    formula="productivity ~ trained + experience",
    unit_fe_variable="worker_id",  # Worker FE
    time_fe_variable="wave",  # Time FE (survey waves)
    fe_method="demeaned",
    model=cp.pymc_models.LinearRegression(sample_kwargs=sample_kwargs),
)

result_workers.summary()

Panel Regression
============================================================
Units: 200 (worker_id)
Periods: 8 (wave)
FE method: demeaned
Observations: 1600
============================================================

Model Coefficients:
Model coefficients:
    Intercept    0.00013, 94% HDI [-0.034, 0.034]
    trained      2.4, 94% HDI [2.3, 2.6]
    experience   0.29, 94% HDI [0.11, 0.47]
    y_hat_sigma  0.73, 94% HDI [0.71, 0.76]

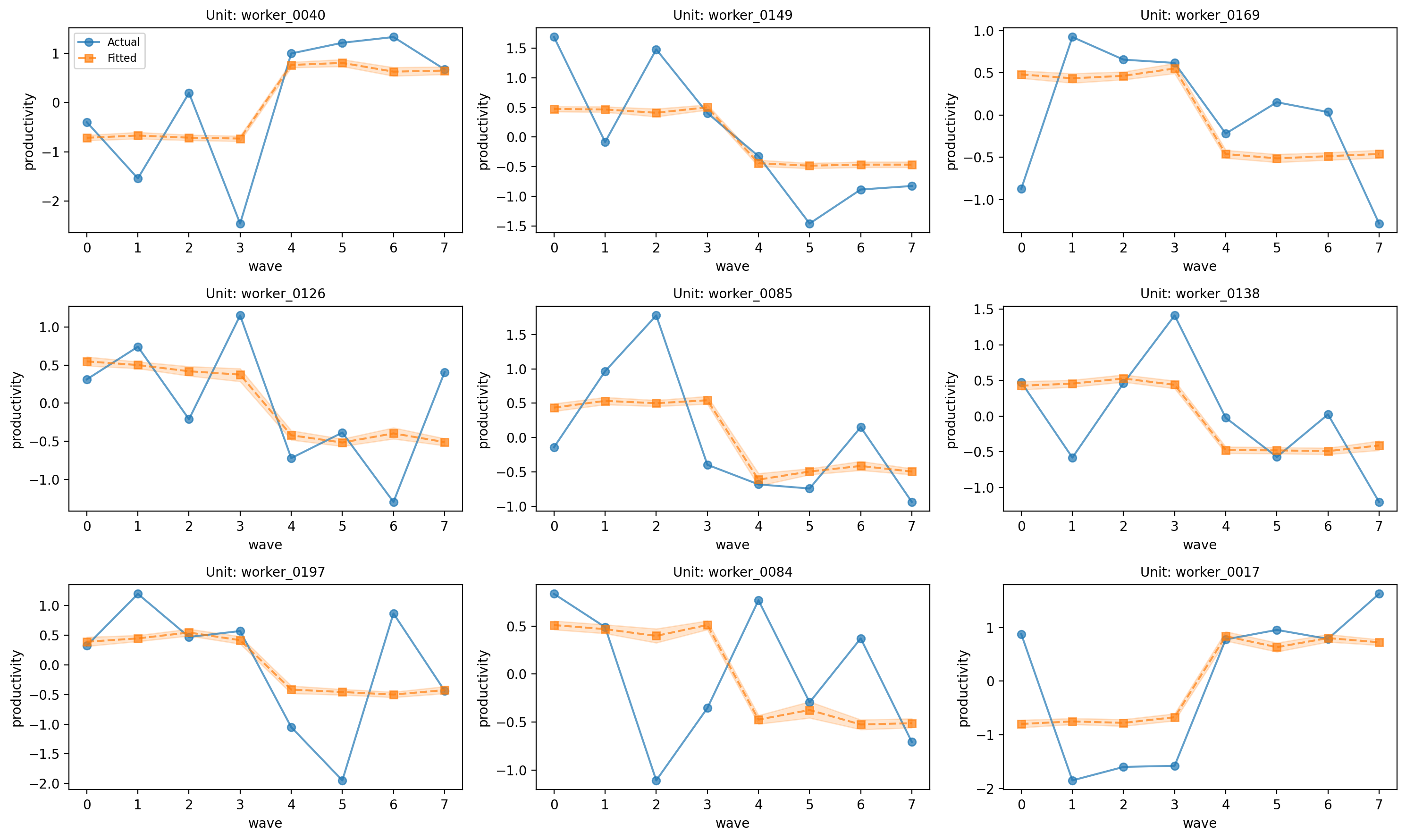
# Worker trajectories
fig, axes = result_workers.plot_trajectories(n_sample=9)
plt.tight_layout()
plt.show()

../_images/e20d03c1d5cf7802f0831da50923801fadb00ed279576b774c05f7d25a404ca0.png

Let’s check some model diagnostics.

# Residuals vs fitted
fig, ax = result_states.plot_residuals(kind="scatter")
plt.tight_layout()
plt.show()

../_images/1cb7c8816dd40f600c3b6a9f5946ad04288a1ff5d28cc7db50a3d66774cad9b8.png

# Distribution of residuals
fig, ax = result_states.plot_residuals(kind="histogram")
plt.tight_layout()
plt.show()

../_images/f16b4b56e467beacdf8ffc5056e177ed36c7227327965dc70d2d54e8262a6d20.png

# Q-Q plot
fig, ax = result_states.plot_residuals(kind="qq")
plt.tight_layout()
plt.show()

../_images/61e1fd9af4204403c8f3179a67c6c8f06a6666e0fccfa6a60d46029e825e6718.png

Summary#

When to use fixed effects#

✅ Use Panel Fixed Effects when:

You have repeated observations on the same units
You suspect time-invariant unobserved confounders
Your treatment varies within units over time
You believe there are no time-varying confounders

❌ Don’t use when:

You only have cross-sectional data
Your treatment is time-invariant (it gets differenced out!)
There are likely time-varying confounders
Outcomes feed back into future treatment

Choosing Your Fixed Effects Specification#

Use this guide to select the appropriate fixed effects for your analysis:

Scenario	Recommended FE	Rationale
Units differ in time-invariant ways only	Unit FE only	Controls for unit heterogeneity; preserves time variation
All units experience common shocks each period	Time FE only	Controls for period effects; preserves cross-sectional variation
Both unit heterogeneity AND common time trends	Two-way FE	Controls for both; standard for DiD-style analyses
Time effects already captured by covariates	Unit FE only	Avoid over-controlling
Treatment is staggered across units	Two-way FE	Essential for valid DiD interpretation

Key Considerations

More FE is not always better: Adding fixed effects removes variation that could be useful for identification. Over-controlling can increase standard errors and even introduce bias.
Think about your DAG: What confounders exist? Are they time-invariant (unit FE), common across units (time FE), or both?
Treatment variation matters:
- If treatment only varies across units (not time), unit FE will absorb all treatment variation!
- If treatment only varies over time (not units), time FE will absorb all treatment variation!
Test sensitivity: When in doubt, run both one-way and two-way FE. If results differ substantially, investigate why.

Dummies vs Within#

Criterion	Dummies	Within
When	Small N (< 100)	Large N (100+)
Pros	Individual unit effects	Scales to large N
Cons	Doesn’t scale	Can’t estimate individual effects
Formula	`y ~ C(unit) + X`	`y ~ X`

Limitations and Caveats#

Before concluding, let’s be explicit about what fixed effects cannot do:

1. Cannot Remove Time-Varying Confounders: As demonstrated in our failure example, if unobserved factors change over time and affect both treatment and outcome, fixed effects will be biased. This is the most common limitation.
1. Cannot Solve Reverse Causality: If the outcome affects future treatment (feedback), fixed effects estimates are biased. Example: if poor sales cause firms to adopt new technology, we cannot estimate the effect of technology on sales using FE.
1. Removes Time-Invariant Variation: Fixed effects identifies effects from within-unit variation only. If your treatment barely varies within units, you have limited identifying variation and imprecise estimates.
1. Assumes Common Time Effects (Two-Way FE): With time fixed effects, you assume all units would follow parallel trends absent treatment. This may not hold if different units have different trajectories.

References#

[1]

Scott Cunningham. Causal inference: The mixtape. Yale university press, 2021.

[2]

Nick Huntington-Klein. The effect: An introduction to research design and causality. Chapman and Hall/CRC, 2021.

[3]

Jeffrey M Wooldridge. Econometric Analysis of Cross Section and Panel Data. MIT Press, 2nd edition, 2010.

[4] (1,2)

Kosuke Imai and In Song Kim. When should we use unit fixed effects regression models for causal inference with longitudinal data? American Journal of Political Science, 63(2):467–490, 2019.

[5]

Clément de Chaisemartin and Xavier D'Haultfœuille. Two-way fixed effects estimators with heterogeneous treatment effects. American Economic Review, 110(9):2964–2996, 2020.